I wrote earlier this year about my attempt to understand the repercussions of toggling 
…which shows how to obtain dozens of program logics just by toggling a handful of switches in the semantics.
However, that diagram is completely terrifying, and (just between you and me) I can’t get my head around much of the rest of Cousot’s paper. So, this blog post is my attempt to end up with a similar diagram to Cousot’s one, but while trying to keep things as simple as possible.
Let us assume that we have a set of states, and that a command is simply a binary relation on states. We shall write 
The original “partial correctness” interpretation [1] of the Hoare triple 
Let us define a helper function: the “strongest postcondition”. We shall write 
We can use 
Flipping the
…is what led O’Hearn to remark that “program correctness and incorrectness are two sides of the same coin”. But there are other components that can be “flipped” too. I think there are three “dimensions” in total:
(NB: Cousot seems to identify four dimensions in his diagram above, but I haven’t understood what his fourth one is.)
The eight options, then, are as follows:
Note that partial correctness can also be rewritten into the more familiar 
…but I quite like how “systematic” the table above is: it distinguishes may from must by negating the pre and postconditions; it distinguishes forward from backward by using 
Note also that I’ve labelled 
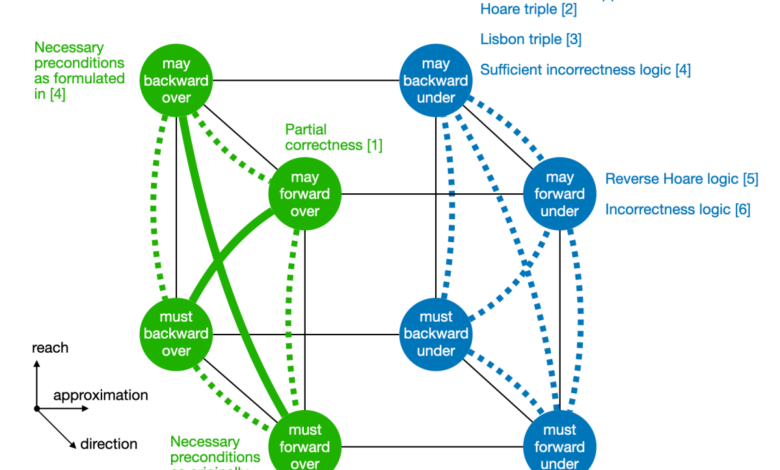
We can assemble all eight options in the table into a cube — a “Hoare cube”, if you will.
In the cube, I’ve drawn solid lines between vertices that represent equal semantics. For instance, may+forward+over is equal to must+backward+over because…
Sometimes these equalities can be phrased as Galois connections. For instance…
…signifies a Galois connection between 
I’ve also drawn dashed lines between vertices that represent equivalent semantics. By “equivalent” here, I mean that there exists a bijection 
For instance, may+backward+over (necessary preconditions, 
may+forward+over (partial correctness, 
…as Ascari et al. have observed [4, Proposition 5.4]. Here we use the bijection 
For another instance, may+forward+under (incorrectness logic, 
may+backward+under (sufficient incorrectness logic, 
For this reason, I’ve deemed all of the over nodes equivalent (and coloured them green) and all of the under nodes equivalent (and coloured them blue).
But is it a bit of a stretch to consider all those same-coloured nodes “equivalent”? I mean, if the point of these bijections is to suggest how a proof in one logic can be transformed into a proof in another logic, then are these transformations reasonable? The bijection 
Still, it does give a pretty handy way to generate proof rules for one logic from the proof rules for another logic. For instance, Ascari et al. [4] present this proof rule from incorrectness logic…
…and if we apply our bijection
…without having to prove anything about its soundness.
To conclude: perhaps program correctness and incorrectness are not simply two sides of the same coin, but two opposite faces of the same cube!
Related work
Möller et al. [2, Section 5] define and briefly study “backward under-approximate Hoare triples”. Zilberstein et al. [3] refer to those triples also as “Lisbon triples”. Ascari et al. [4] define sufficient incorrectness logic as a proof system for those “backward under-approximate Hoare triples”, and I’m grateful to Ike Mulder who referred me to Ascari et al.’s paper in a comment on my earlier blog post.
Zilberstein et al. [3] defines and studies “Outcome logic”, but I haven’t included it in my “cube” because I don’t think it quite fits with the other logics – its postconditions are not simply “sets of states”, but have a more complicated monoidal structure. I also haven’t included “Exact separation logic” [11], which unifies over-approximate and under-approximate reasoning in the context of separation logic.
Zhang and Benjamin Kaminsky [8, Section 6.3] also studied the eight options in my table above, similarly obtained by toggling three binary switches (albeit with slightly different names), and I’m grateful to Benjamin for pointing me to his work in a comment on my earlier blog post. I’ve reproduced their table here:
The two blue rows in their table are equal, and they correspond to the two “partial correctness” vertices in my cube. The two orange lines are also equal, and they correspond to the two “necessary preconditions” vertices in my cube. I also haven’t got names for the ??? and ¿¿¿ logics, but I note that ??? can be straightforwardly obtained from sufficient incorrectness logic via the
For the record: one potential point of confusion in Zhang and Kaminsky’s table is that what they call “wp” is actually what O’Hearn [6, Section 6.3] calls the “weakest possible precondition”: the sets of states from which
Bibliography
- [1] C.A.R. Hoare: An axiomatic basis for computer programming. CACM, 1969.
- [2] Bernhard Möller, Peter O’Hearn, and Tony Hoare: On Algebra of Program Correctness and Incorrectness. RAMiCS, 2021.
- [3] Noam Zilberstein, Derek Dreyer, and Alexandra Silva: Outcome Logic: A Unifying Foundation for Correctness and Incorrectness Reasoning. OOPSLA, 2023.
- [4] Flavio Ascari, Roberto Bruni, Roberta Gori, and Francesco Logozzo: Sufficient Incorrectness Logic: SIL and Separation SIL. ArXiv, 2023.
- [5] Edsko de Vries and Vasileios Koutavas: Reverse Hoare Logic. SEFM, 2011.
- [6] Peter O’Hearn: Incorrectness Logic. POPL, 2020.
- [7] Patrick Cousot, Radhia Cousot, Manuel Fähndrich, Francesco Logozzo: Automatic Inference of Necessary Preconditions. VMCAI, 2013.
- [8] Linpeng Zhang and Benjamin Lucien Kaminsky: Quantitative Strongest Post. OOPSLA, 2022.
- [9] C.A.R. Hoare: Some properties of predicate transformers. JACM, 1978.
- [10] Patrick Cousot: Calculational Design of [In]Correctness Transformational Program Logics by Abstract Interpretation. POPL, 2024.
- [11] Petar Maksimovic, Caroline Cronjäger, Andreas Lööw, Julian Sutherland, and Philippa Gardner: Exact Separation Logic: Towards Bridging the Gap Between Verification and Bug-Finding. ECOOP, 2023.
