The Art and Mathematics of Genji-Kō


You might think there’s unlikely to be any interesting mathematics arising from
incense appreciation, but that’s only because you’re unfamiliar with the
peculiar character of Muromachi (室町) era (circa 1300-1500) Japanese nobles.
There has never been a group of people in any time or place who were so keen to
display their sophistication and refinement. It wouldn’t do to merely put out a
few sticks of incense – no, you would have to prove that your taste was more
exquisite, your judgement more refined, your etiquette more oblique. You could
of course merely invite some other nobles over for an incense appreciation
party, make a few cutting but plausibly deniable remarks about a rival, maybe
drop a few lines of poetry linking the incense to the current season. But if
you were really on the ball you’d be looking for a way to simultaneously
humiliate your rivals, flirt with your love interest, and impress people in a
position of power. They didn’t just perfect cultured refinement – they
weaponized it.
Only under such conditions could something like Genji-kō (源氏香) arise. It is
a parlor game played with incense – just one of many similar games inside the
broader umbrella of kōdō (香道), the traditional Japanese art of incense
appreciation.
What sets Genji-kō apart is its extreme difficulty – where another kōdō game
might have contestants write down their guesses for three separate incenses and
score a point for each correct guess, Genji-kō asks contestants to smell five
separate samples, then determine which of the five are the same. All five might
be the same, all five might be different, or (and this is where it gets
interesting) they might be in groups of two or three or four. For example, the
correct solution might be that the first and fourth are the same, the second
and fifth are the same, and the third in a group by itself. Or any other
possible combination of groupings.
Contestants score a single point if they correctly group all five incenses;
otherwise they score nothing. A typical game has five rounds over the course of
an evening, with an overall winner declared at the end.
Obviously contestants would need some kind of notation to record their answers
in a concise, unambiguous, and easy to read way, and it is really about this
notation – and the art, mathematics, and culture connected to it – that this
article is about.
Notation
The solutions that Genji-kō players submit are called Genji-mon (源氏紋) and
are drawn with exactly five vertical lines, representing the five possible
incenses. To show that two or more incenses are part of the same group, you
draw a horizontal line connecting the top of every vertical line in that group.
To avoid confusion when there are two or more groups, you draw these horizontal
lines at different heights, shortening the vertical lines as needed:
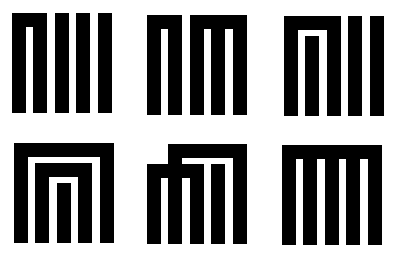
There are a few nuances worth mentioning. If two groups don’t overlap, there is
no need draw them at different heights (top center.) If one group is
“contained” inside another, the inner group is drawn at the lower height (top
right, bottom left) so that it appears nested inside the other. Sometimes it is
impossible to avoid an intersection (bottom center) but it is clear that groups
are distinct because the horizontal connecting lines are at different heights.
Genji-Kō features as a plot point in episode 8 of the experimental horror
anime Mononoke, where it is suggested that players used blocks to
record their solutions:
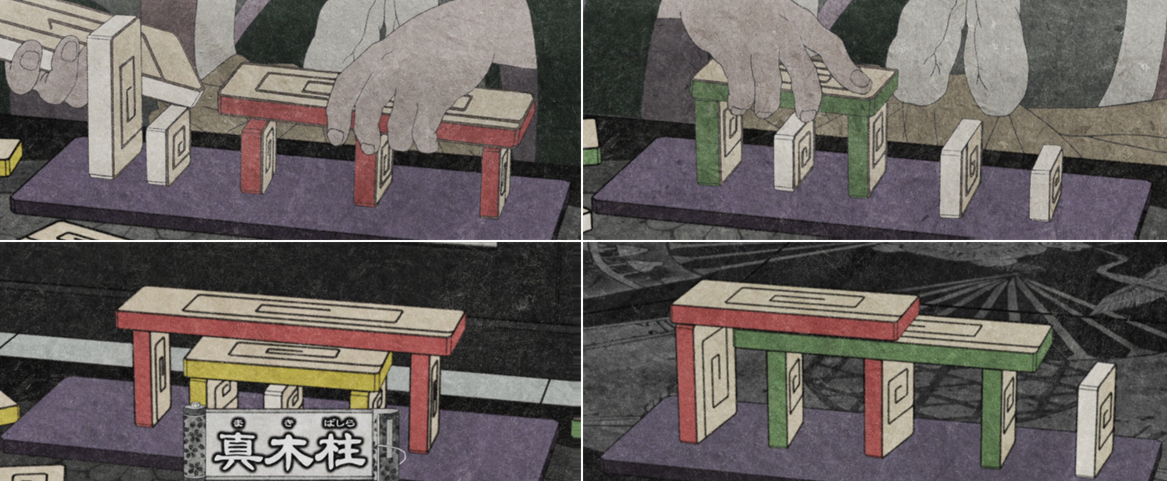
While this might be true – the episodes description of Genji-Kō is otherwise
grounded and well-researched – I haven’t seen any other references to this;
everything else I’ve seen says the game was played with ink and paper. I think
it’s probably just a case of artistic license – the blocks were more visually
interesting to animate.
Etymology
Genji-kō, by the way, is named after the titular Genji of the Heian (平安) era
literary classic The Tale of Genji. (The fact that “Genji” is a proper
name is also why I capitalize Genji-kō and Genji-mon.)
There are two connections. First, in one chapter of the book Genji hosts an
incense appreciation party. Second, since there are 52 possible patterns and 54
chapters of the book, each Genji-mon is traditionally associated with – and
named after – a chapter, except for the first and last chapters, which are
omitted.
Every educated person of the Muromachi era would be intimately familiar with
The Tale of Genji and would know the themes, season, and characters
associated with each chapter by heart, giving each pattern a literary
resonance. A skillful kōdō practitioner hosting a game of Genji-kō would choose
a solution that referenced the current season or recent event, adding both a
layer of meaning to the game and a hint to other skilled players.
There are several different words we could use to refer
to the patterns themselves, but I’ve chosen Genji-mon as it seems to be the
most common.
Cultural Influence
Compared to other traditional arts from the same era such as tea ceremony or
flower arranging, kōdō is not particular popular or well-known even in Japan;
nevertheless it is still played even to this day.
However, its cultural influence extends beyond the few who actually play the
game – the patterns show up fairly often as a motif in contemporary Japanese
graphic design, and it’s especially popular on traditional goods such as
kimono:


While
cheaper fabrics
simply print the same Genji-mon repeatedly, high-quality Genji-Kō textiles will
use a variety of Genji-mon so that the pattern seems to never quite repeat:

Naturally, Genji-mon are often found on good related to incense in some way,
such as this kōdō set, incense box, or incense holder:
In the 1840’s Kunisada painted a series of wall scolls, one for each
chapter of The Tale of Genji, and included the associated Genji-mon on
each:
Drawing Genji-Mon
To draw Genji-Mon programatically, we’ll use the standard recursive algorithm
to generate all possible partitions for a set of five elements:
def partitions(s: Set[int]) -> Iterator[List[Set[int]]]:
"""Yield all partitions of a set as they are generated."""
if not s:
yield []
return
first = next(iter(s))
rest = s - {first}
for partition in partitions(rest):
yield [{first}] + partition
for i in range(len(partition)):
new_partition = (
partition[:i] +
[partition[i] | {first}] + partition[i+1:]
)
yield new_partition
However, the partition alone does not suffice to fully characterize a Genji-mon.
While we must draw overlapping groups at different heights to avoid ambiguity,
there is still a free choice about which groups we make taller. After studying
the chart of traditional Genji-mon, two rules became clear:
- Groups should be as tall as possible.
- Groups entirely inside† other
groups should be lower and appear to nest inside the outer group.
I implemented this as a simple brute-force cost-based optimizer, because that
made it easy to experiment with different rules. (Even though in the end I
only used those two simple rules, I experimented with many others trying to
get rid of the remaining special cases, which I’ll discuss below.)
def optimal_genjiko_for_partition(
partition: List[Set[int]]
) -> List[Tuple[float, Set[int]]]:
"""
Given a partition, find the optimal Genji-kō layout by minimizing a cost
function.
"""
best_cost = math.inf
best_genjiko = None
HEIGHTS = [1.0, 0.8, 0.6]
# Generate all possible combinations of heights
for height_combo in itertools.product(HEIGHTS, repeat=len(partition)):
genjiko_candidate = [
(height, group)
for height, group
in zip(height_combo, partition)
]
# Skip invalid configurations
if not validate_genjiko(genjiko_candidate):
continue
# Encourage larger heights
cost = -sum(height for height, _ in genjiko_candidate)
for height1, group1 in genjiko_candidate:
for height2, group2 in genjiko_candidate:
# Large penalty for higher inner group height
if is_nested_within(group1, group2) and height1 > height2:
cost += 1
# keep track of the best solution so far
if cost < best_cost:
best_cost = cost
best_genjiko = genjiko_candidate
return best_genjiko
Actually drawing these using Pillow or organizing them into a
grid is straight-forward, so you can check the source code if you’re
interested in those details.
Here’s what we get if always use the algorithmically calculated “optimal”
layout and simply put them in the order returned by partitions():

Good, but not perfect. The order is only vaguely similar, and the four Genji-mon
rendered in red are the ones where our “optimal” layout has failed to reproduce
the traditional design.
Genji-mon Order
Knuth mentions that the Genji-mon “were not arranged in any particularly
logical order” and I’m inclined to agree. I tried several variations of the
above partition() function hoping to find one where the traditional order
would just fall out naturally, but it never did. A close inspection of the
traditional order makes it clear that this was never going to happen: While
there is an overall trend from many to fewer groups, there are just too many
cases where the order is clearly arbitrary.
I found a several references that put the Genji-mon in a different order, and
even some that tried to stretch it to 54 using some kind of
duplication
or introducing
irregular
patterns.*
If we recall the original purpose they served in the game, though, this is
clearly nonsense, not to mention being both mathematically impossible and at
odds with tradition.
However, the association between the 52 patterns and chapter titles for
chapters 2-53 of the Tale of Genji seems watertight and consistent for
centuries back. Also, the order of the chapters is mostly consistent across
sources (there is some disagreement about the order of the later chapters, and
one chapter which survives only as a title or perhaps was intentionally elided
as a delicate way to elude to a character’s death) so I’ve put my Genji-mon in
chapter order. You can find the full table in Appendix C.
Special Cases
I spent some time trying to find some elegant heuristic that would nudge
the layout algorithm to produce those four without breaking any of the others,
but the rules were more complex than simply listing the special cases (and
none of them correctly handled Yūgiri (夕霧) which I’ll discuss below.)
The four special cases are:
# Suma: {1, 3, 4} should be lower than {2, 5}
df.at[10, "Layout"] = [ (0.8, {1, 3, 4}), (1.0, {2, 5}) ]
# Hatsune: {1, 3} should be lower than {2, 4}
df.at[21, "Layout"] = [ (0.8, {1, 3}), (1.0, {2, 4}), (1.0, {5}) ]
# Yuguri: {1, 4} should be lower than {3, 5}, and {2} even lower.
df.at[37, "Layout"] = [ (0.8, {1, 4}), (0.6, {2}), (1.0, {3, 5}) ]
# Nioumiya: {1, 2, 4} should be lower than {3, 5}
df.at[40, "Layout"] = [ (0.8, {1, 2, 4}), (1.0, {3, 5}) ]
With these corrections, and using the Tale of Genji chapter order:

Of the four exceptions, two are obvious improvements (fixing the “hole” in Suma
and the “dent” in Hatsune) and one (Nioumiya) is a matter of indifference.
However, the fourth, Yugiri, seems to actively violate the basic rules around
nesting and creates a three-level structure when two would have sufficed:

The cost-based optimizer would have never chosen that layout because its most
basic tenet is to make the groups as tall as possible. A heuristic, let me
remind you, that holds for the other 51 Genji-mon. However, all the examples
of Yuguri I found online use the traditional design, such as this
wall scroll
by Kunisada or this woodblock print by Masao Maeda:
So I don’t think I have a leg to stand on unless I want to spit in the face of
hundreds of years of tradition; we’ll just have to hard-code Yuguri as a
special case.
Counting Genji-Mon
The connection between Genji-kō and mathematics becomes apparent if we ask
ourselves, “Why are there exactly 52 Genji-mon patterns? How can we be sure
there aren’t more?”
Like a lot of questions in mathematics, it helps to generalize things. Instead
of focusing on five incenses, let’s ask ourselves, how many unique ways are
there of grouping $n$ elements? This lets us ease into the problem, starting
with a simpler case and building complexity gradually.
For $n = 1$, there’s clearly only solution:

For $n = 2$, there are only two possible solutions. Either the first element is
in a group by itself, or it is in a group with another.

For $n = 3$, things start to get more interesting. Let’s repeat the trick we
used for $n = 2$ and focus on the first element. It must either be in a group
by itself, in a pair with another, or in the same group as all others. That
gives us exactly three cases to consider:
- If it is in a group by itself, there there are two elements left over, and
we already know that there are two ways to group those two remaining
elements. - If it in a pair, then we have a choice: we can either pair it with the
second or third element. In either case there will only be one element left
over. - And there is only one way to have all the elements be in the same
group.
Here they all are, in Genji-kō notation:

Thus we have $1 \times 2 + 2 \times 1 + 1 = 5$ ways to partition a set of
three elements.
This is starting to look like a repeatable strategy. We always start by
focusing on the first element. We can neatly divide the set of all possible
solutions by the size $k$ of the group containing this first element. For each
$k$ between $1$ and $n$, there are two questions to ask:
- How many ways are there of choosing the set that contains the first element?
- How many ways are there of putting the remaining $n-k$ elements into groups?
Let’s try that out for $n = 4$. The other cases are obvious, but let’s focus on
the case where $k = 2$ as there’s a new wrinkle there. We have to choose one
other element from three possible elements, so there are three ways of doing
that. We’ll always have two left over, and there are always two ways of
grouping those together. This these are two independent choices – choosing the
first group, then choosing how to partition the remaining elements, there are
$3 \times 2 = 6$ ways of doing that. This case teaches us that we have to count
both the ways of selecting a set of $k$ elements, and the ways to group the
remaining elements, and multiply them together.
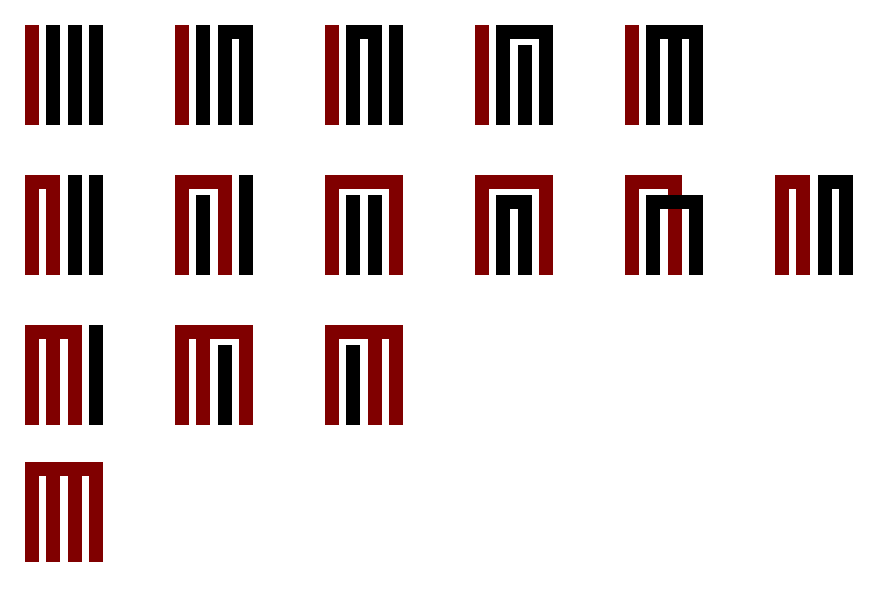
So, for $n = 4$, there are $1 \times 5 + 3 \times 2 + 3 \times 1 + 1 = 15$
possible solutions.
Mathematical Approach
For the case of $n = 5$, I’ve
generated the diagram
showing how to use the same strategy to count all possible Genji-mon,
but I think it’s more useful to take the strategy we’ve learned and abstract it.
First, let’s use the right terminology. What we’ve so far called a “Genji-mon,”
mathematicians would call a partition. In mathematical terms, the question
we’re asking is, “How many distinct partitions are there for a set of $n$ elements?”
This number also has a name: the Bell number denotated $B_n$.
Above, we brute-forced a calculation for $B_1$ through $B_4$ using a mix of
intuition and common sense. To formalize the strategy we discovered by doing
that into mathematical notation we’ll need one concept you may or may not have
seen: “the number of ways to choose $k$ elements from $n$ distinct elements,
ignoring order” is called “$n$ choose $k$” or the binomial coefficient
and is denoted $nCk$ or with this tall bracket notation:
\[
\binom{n}{k} = \frac{n!}{k! (n-k)!}
\]
There are many ways of deriving the equation in terms of factorials, but here’s
one I like: imagine we put all $n$ elements in order; there are $n!$ ways of
doing that. Then we always take the $k$ leftmost elements for our choice. However,
because order doesn’t matter, we divided by all the different ways of ordering
the $k$ chosen elements, which is $k!$, and the $n-k$ remaining elements, which
is $(n-k)!$.
With that tool in hand, we start can start to define the Bell numbers. The first
couple can be treated as special cases, since obviously there’s only one way
to partition a set of zero or one elements:
\[
B_0 = 1, B_1 = 1
\]
For $n > 1$, we generalize the strategy we discovered above:
- Pick an arbitrary element to represent the “first element.”
- We’ll call whichever set in the partition that contains this first element
the “first set.” Every element is in exactly one set of the partition, so this
uniquely picks out a particular set in the partition. - For each $k$ between $1$ and $n$, consider only partitions where the first
set is of size $k$. This divides the problem up into non-overlapping buckets:
if two partitions have different sized first set, they cannot
possibly be the same. - We have to make a choice about the other $k-1$ elements to include in the
first set, and there are $\binom{n-1}{k-1}$ ways of doing that. - Regardless of which elements we choose for the first set, there will
be $n-k$ elements left over. They won’t always be the same elements,
but there will always be $n-k$ of them. Thankfully, we already know how many ways
there are to partition a set of $n-k$ elements: it’s $B_{n-k}$. - Since our choices for step 4 and step 5 are independent, we can multiply
the two counts together to get the total number of partitions where the
first set is of size $k$. - Finally, we just have to add up everything for $k$ from $1$ to $n$.
In concise mathematical notation, this algorithm is:
\[
B_{n} = \sum_{k=1}^{n} \binom{n-1}{k-1} B_{n-k} \tag{1}
\]
We can make this a little neater if we run $k$ from $0$ to $n-1$ instead and
use the fact that $\binom{n}{r} = \binom{n}{n-r}$ to count down instead of up:
\[
B_{n} = \sum_{k=0}^{n-1} \binom{n-1}{k} B_{k} \tag{2}
\]
Substituting $n+1$ for $n$ we can put the recurrence relation in an even tidier
form, which is the canonical form you’ll find in textbooks:
\[
B_{n+1} = \sum_{k=0}^n \binom{n}{k} B_k \tag{3}
\]
Equation $(3)$ looks a little cleaner and easier to work with, and can be
understood intuitively if you reconceptualize $k$ not as the number of elements
in the first group, but as the number of elements not in the first group.
Shifting to calculating $B_{n+1}$ also allows us to get rid of the “minus
ones” in the original that made the expression seem messy. However, it’s a
little divorced from the intuition about pinning the size of the first set we
used to motivate $(1)$ although of course they’re completely equivalent
mathematically.
Of these three equivalent equations, $(2)$ is the most natural fit for a Python
implementation because range(n) naturally runs from 0 to n-1 and it makes
far more sense to implement a function for $B_n$ instead of $B_{n+1}$:
def bell_number(n: int) -> int:
"""Calculate the Bell number for any integer `n`."""
if n < 0:
raise ValueError("The Bell number is not defined for n < 0.")
elif n < 2:
return 1
else:
return sum(
comb(n-1, k) * bell_number(k)
for k in range(n)
)
(Optimizing this function is left as a exercise to the reader, who may find the
techniques described in my earlier article on writing a fairly fast Fibonacci
function helpful.)
We can use it to calculate the first 20 Bell numbers:
| $n$ | $B_n$ |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 5 |
| 4 | 15 |
| 5 | 52 |
| 6 | 203 |
| 7 | 877 |
| 8 | 4,140 |
| 9 | 21,147 |
| 10 | 115,975 |
| 11 | 678,570 |
| 12 | 4,213,597 |
| 13 | 27,644,437 |
| 14 | 190,899,322 |
| 15 | 1,382,958,545 |
| 16 | 10,480,142,147 |
| 17 | 82,864,869,804 |
| 18 | 682,076,806,159 |
| 19 | 5,832,742,205,057 |
| 20 | 51,724,158,235,372 |
And there it is: $B_5 = 52$, so there are exactly 52 Genji-mon, no more and
no fewer.
Conclusion
It’s not too surprising that some of these mathematics were worked out over
seven hundred years ago; combinatorics is an easy branch to stumble into when
it arises in connection to some practical problem. It does, however, feel
slightly surreal that it was a bunch of bored nobles playing an esoteric parlor
game who first noticed these patterns and used it to attach literary
significance to their activities. But I’m happy they did so, because they did
something we mere number crunchers would not have thought to do: they made them
beautiful.
Appendices
Appendix A: Source Code
The full source code use for this article is available on GitHub. The
main Python code is in src/genjiko.py and the notebooks
directory contains many examples of usage.
Appendix B: Alternative Genji-Kō Chart
Genji-mon are often rendered with thick lines which achieves an interesting
effect with the negative space. By playing around with the parameters a little:
genjiko_df = load_genjiko()
genjiko_df['Color'] = "black"
draw_annotated_genjiko_grid(
genjiko_df,
cell_size=82,
grid_width=8,
grid_height=7,
line_width=14,
padding=20,
include_index_label=False,
include_romaji_label=False,
grid_indent=1,
)
We can achieve a very attractive result:

Appendix C: Full Table
Here is the full table in HTML format, so you can copy-and-paste the kanji and other
fields. The Genji-mon column uses the Genji-Kō TrueType font available from
illllli.com.
You can also download this same table as a UTF-8 encoded CSV file
or Excel spreadsheet.
| Chapter | Kanji | Romaji | English | Partition | Genji-mon |
|---|---|---|---|---|---|
| 2 | 帚木 | Hōkigi | The Broom Tree | {1}, {2}, {3}, {4}, {5} | B |
| 3 | 空蝉 | Utsusemi | Utsusemi | {1}, {2}, {3}, {4, 5} | C |
| 4 | 夕顔 | Yūgao | Yūgao | {1}, {2}, {3, 4}, {5} | D |
| 5 | 若紫 | Wakamurasaki | Young Murasaki | {1}, {2, 3}, {4, 5} | E |
| 6 | 末摘花 | Suetsumuhana | The Saffron Flower | {1, 2, 3, 4}, {5} | F |
| 7 | 紅葉賀 | Momijinoga | The Festival of Red Leaves | {1}, {2, 3, 5}, {4} | G |
| 8 | 花宴 | Hana no En | The Flower Feast | {1}, {2}, {3, 5}, {4} | H |
| 9 | 葵 | Aoi | Aoi | {1, 2}, {3}, {4}, {5} | I |
| 10 | 賢木 | Sakaki | The Sacred Tree | {1, 2, 3}, {4, 5} | J |
| 11 | 花散里 | Hana Chiru Sato | The Village of Falling Flowers | {1}, {2, 4}, {3, 5} | K |
| 12 | 須磨 | Suma | Exile at Suma | {1, 3, 4}, {2, 5} | L |
| 13 | 明石 | Akashi | Akashi | {1}, {2, 3}, {4}, {5} | M |
| 14 | 澪標 | Miotsukushi | The Flood Gauge | {1}, {2, 4, 5}, {3} | N |
| 15 | 蓬生 | Yomogiu | The Palace in the Tangled Woods | {1, 2, 3}, {4}, {5} | O |
| 16 | 関屋 | Sekiya | A Meeting at the Frontier | {1}, {2, 3, 4}, {5} | P |
| 17 | 絵合 | Eawase | The Picture Competition | {1, 3}, {2, 5}, {4} | Q |
| 18 | 松風 | Matsukaze | The Wind in the Pine Trees | {1, 2}, {3, 4}, {5} | R |
| 19 | 薄雲 | Usugumo | A Wreath of Cloud | {1}, {2, 3, 4, 5} | S |
| 20 | 朝顔 | Asagao | Asagao | {1, 3, 4}, {2}, {5} | T |
| 21 | 乙女 | Otome | The Maiden | {1, 3}, {2}, {4}, {5} | U |
| 22 | 玉鬘 | Tamakazura | Tamakatsura | {1, 2}, {3, 4, 5} | V |
| 23 | 初音 | Hatsune | The First Song of the Year | {1, 3}, {2, 4}, {5} | W |
| 24 | 胡蝶 | Kochō | The Butterflies | {1, 4}, {2, 3, 5} | X |
| 25 | 蛍 | Hotaru | The Glow-Worm | {1, 2, 4}, {3}, {5} | Y |
| 26 | 常夏 | Tokonatsu | A Bed of Carnations | {1}, {2}, {3, 4, 5} | Z |
| 27 | 篝火 | Kagaribi | The Flares | {1}, {2, 4}, {3}, {5} | a |
| 28 | 野分 | Nowaki | The Typhoon | {1, 2}, {3}, {4, 5} | b |
| 29 | 御幸 | Miyuki | The Royal Visit | {1, 3}, {2, 4, 5} | c |
| 30 | 藤袴 | Fujibakama | Blue Trousers | {1, 4}, {2}, {3}, {5} | d |
| 31 | 真木柱 | Makibashira | Makibashira | {1, 5}, {2, 4}, {3} | e |
| 32 | 梅枝 | Umegae | The Spray of Plum Blossom | {1, 2, 3, 5}, {4} | f |
| 33 | 藤裏葉 | Fuji no Uraba | Fuji no Uraba | {1}, {2, 5}, {3, 4} | g |
| 34 | 若菜上 | Wakana Jō | Wakana, Part I | {1, 2, 5}, {3, 4} | h |
| 35 | 若菜下 | Wakana Ge | Wakana, Part II | {1, 3}, {2}, {4, 5} | i |
| 36 | 柏木 | Kashiwagi | Kashiwagi | {1, 3, 5}, {2}, {4} | j |
| 37 | 横笛 | Yokobue | The Flute | {1, 4, 5}, {2}, {3} | k |
| 38 | 鈴虫 | Suzumushi | The Bell Cricket | {1, 5}, {2}, {3, 4} | l |
| 39 | 夕霧 | Yūgiri | Yūgiri | {1, 4}, {2}, {3, 5} | m |
| 40 | 御法 | Minori | The Law | {1, 4}, {2, 5}, {3} | n |
| 41 | 幻 | Maboroshi | Mirage | {1, 5}, {2}, {3}, {4} | o |
| 42 | 匂宮 | Nioumiya | Niou | {1, 2, 4}, {3, 5} | p |
| 43 | 紅梅 | Kōbai | Kōbai | {1}, {2, 5}, {3}, {4} | q |
| 44 | 竹河 | Takekawa | Bamboo River | {1, 5}, {2, 3, 4} | r |
| 45 | 橋姫 | Hashihime | The Bridge Maiden | {1, 3, 4, 5}, {2} | s |
| 46 | 椎本 | Shiigamoto | At the Foot of the Oak Tree | {1, 4}, {2, 3}, {5} | t |
| 47 | 総角 | Agemaki | Agemaki | {1, 4, 5}, {2, 3} | u |
| 48 | 早蕨 | Sawarabi | Fern Shoots | {1, 2}, {3, 5}, {4} | v |
| 49 | 宿木 | Yadorigi | The Mistletoe | {1, 2, 4, 5}, {3} | w |
| 50 | 東屋 | Azumaya | The Eastern House | {1, 2, 5}, {3}, {4} | x |
| 51 | 浮舟 | Ukifune | Ukifune | {1, 5}, {2, 3}, {4} | y |
| 52 | 蜻蛉 | Kagerō | The Gossamer Fly | {1, 3, 5}, {2, 4} | z |
| 53 | 手習 | Tenarai | Writing Practice | {1, 2, 3, 4, 5} | 1 |
Note that whenever the English column has apparently been left untranslated,
this is because the chapter title is the proper name of one of the characters
from The Tale of Genji. Translating these would be as nonsensical as
translating “Jack Smith” to “Lifting Device Metal Worker.”
Appendix D: Names for Genji-Kō Pattern
This table is included merely to illustrate the variety of legitimate ways
to refer to the patterns used in Genji-kō, and to justify my choice to
standardize on Genji-mon. Click on any of the kanji to link directly to
the Google Image Search for that name.
Appendix E: Asymptotic Behavior
The Bell numbers grow very fast. The asymptotic growth is approximately:
\[
B_n \sim \frac{1}{\sqrt{2 \pi n}} \left( \frac{n}{\ln n} \right)^n
\]
Which is just a tiny bit slower than factorials, as you can see if you compare
it to Stirling’s approximation.






