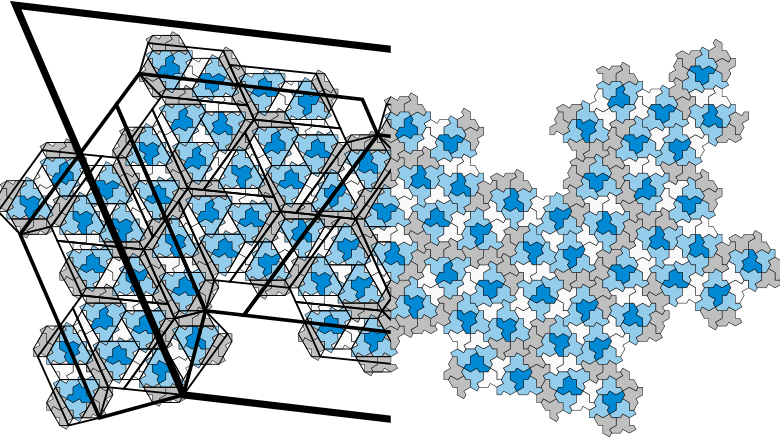
An aperiodic monotile

David Smith, Joseph Samuel Myers, Craig S. Kaplan, and
Chaim Goodman-Strauss, 2023

An aperiodic monotile, sometimes called an “einstein”, is a shape
that tiles the plane, but never periodically. In this paper we
present the first true aperiodic monotile, a shape that forces
aperiodicity through geometry alone, with no additional constraints
applied via matching conditions. We prove that this shape, a polykite
that we call “the hat”, must assemble into tilings based on a substitution
system. The drawing above shows a patch of hats produced using a few
rounds of substitution.

This page collects the resources associated with this work. We invite
you to look at all of the following.

Tools and links

• Our article was published in the journal Combinatorial Theory
  In June, 2024 (Volume 4, Issue 1). You can read the the article
  on their site,
  or visit the (identical)
  preprint on the
  arXiv.

• In May we published a follow-up paper,
  A chiral aperiodic monotile,
  in which we exhibit shapes that tile aperiodically without
  reflections. Please visit the page about that paper for
  more information.

• The hat is one member of a continuous family of shapes that are all
  aperiodic, and that all tile the plane in the same way. We have
  created an animation that moves smoothly through this family of shapes.
  You can
  watch it
  on YouTube, or download your own copy
  (which you can more easily watch looped).

• You can create your own patches of hats, and save them as PNG or
  SVG files, using an interactive application
  that runs in your web browser. You can also get your own copy of the
  source code
  (with a BSD 3-clause license).

• Separately, we have created a
  second interactive application that lets you
  construct patches of hats based on the H7/H8 substitution rules shown
  in Figure 2.11 of the paper. This application includes a particularly
  useful feature, a slider that lets you move through the continuum of
  shapes mentioned above.

• In the paper we give two different proofs of aperiodicity. One
  of them relies on a computer-assisted case-based analysis.
  For validation purposes, we re-implemented this analysis as a Python
  program. You can download the source code
  for this program, run
  it yourself, and check its correctness.

Other resources

Sample images

Here are some sample images you can use in publications, media, etc.
Feel free to modify these images to suit your tastes.

All images, and the MP4 animation above, are licensed under a Creative Commons Attribution 4.0 International License.

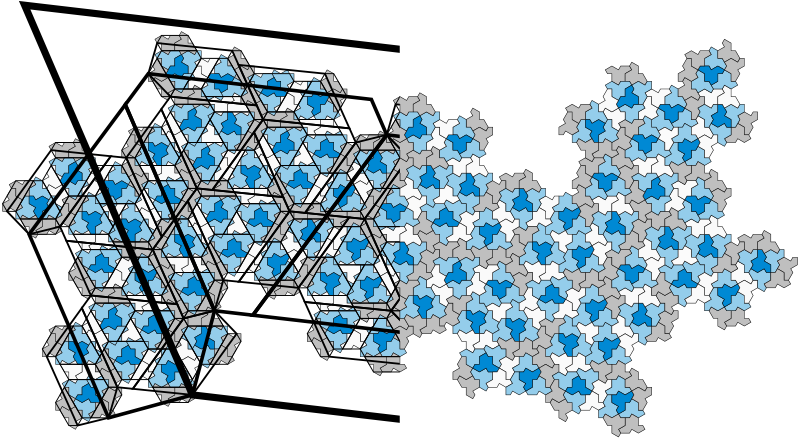
A still more zoomed out patch with the same colouring as the first example,
with a local centre of threefold rotation in the centre of the drawing.

[1200×1200 PNG] [Scalable PDF]

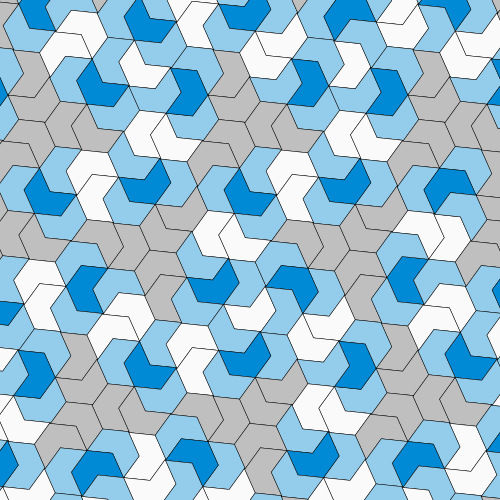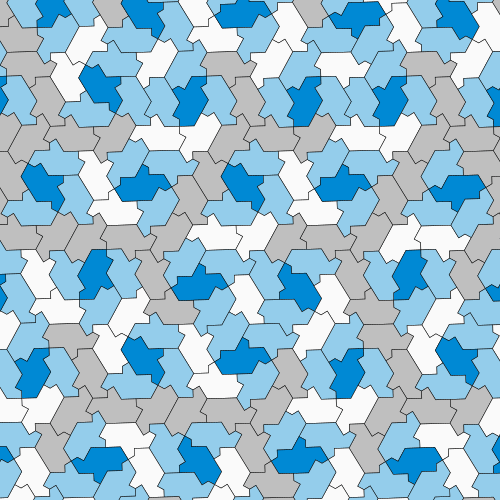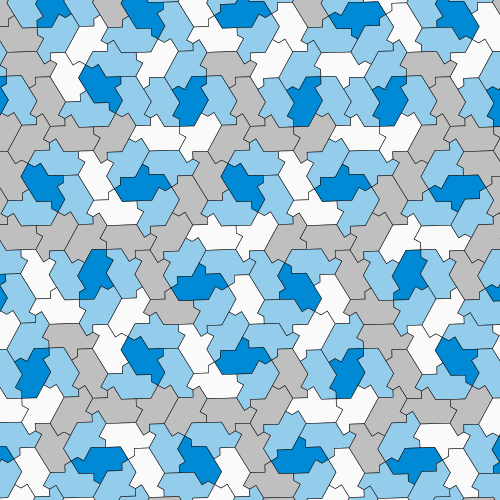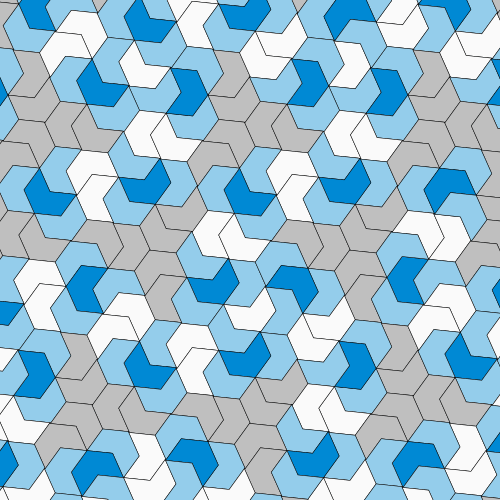
A looping animated GIF similar to the animation mentioned above.
[500×500 GIF]

If you would like to contact us about this paper, please email me at
csk@uwaterloo.ca.